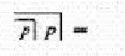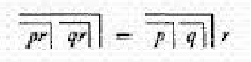Ultimate Simplicity of Logic
Armahedi Mahzar (c) 2011
Logic in history has many formulations. The first formulation is verbal as it is formulated by Aristotle 
, the founder of logic as a science. It is so wordy, so medieval logicians had to invent mnemonic for all valid syllogism that was discovered by the founder and combined them in a poem that has to be memorized by the students of logic. The mnemonic is systematic but it is hard to be understood. Fortunately, later on people try to make logic as easy as arithmetic. The first one who succeed to formulate logic mathematically is George Boole. Some people try to simplify the Boolean algebra to the ultimate simplicity.
BOOLEAN LOGICAL ALGEBRA
George Boole 
is known as the first man who succeed to treat logic mathematically.
He symbolized
logical a OR b with the symbol of arithmetical adddtion a + b,
logical a AND b with the symbol of arithmetical multiplication a X b and
logical NOT a with the the symbol of arithmetical complementation 1 – aIt is a genial step to mathematize logic. All the arithmetcal rules ar followed,
but some strange forms are generated like
a X a = a + a = a (Law of idempotency)
so we have
(1-a) X a = 0 (Law of contradiction)
(1-a) + a = 1 (Law of Complementation)All we need to know is to memorize table of operation to logical values
NoT operation
(1) 1-1=0
(2) 1-0=1AND operation
(3) 1X1=1
(4) 1X0=0
(5) 0X1=0
(6) 0X0=0OR operation
(7) 1+1=1
(8) 1+0=1
(9) 0+1=1
(10) 0+0=0I think it is easy to memorize, if we remember the following rule
“all logical operation entries is similar to arithmetical entries,
but the OR operation of 1 + 1 which is equal 1 rather than 2″But we do not have to remember the rule if we just define the logical addition in term of logical multiplication and logical complementation like thisx+y == 1-(1-x)(1-y)
logical a OR b with the symbol of arithmetical adddtion a + b,
logical a AND b with the symbol of arithmetical multiplication a X b and
logical NOT a with the the symbol of arithmetical complementation 1 – aIt is a genial step to mathematize logic. All the arithmetcal rules ar followed,
but some strange forms are generated like
a X a = a + a = a (Law of idempotency)
so we have
(1-a) X a = 0 (Law of contradiction)
(1-a) + a = 1 (Law of Complementation)All we need to know is to memorize table of operation to logical values
NoT operation
(1) 1-1=0
(2) 1-0=1AND operation
(3) 1X1=1
(4) 1X0=0
(5) 0X1=0
(6) 0X0=0OR operation
(7) 1+1=1
(8) 1+0=1
(9) 0+1=1
(10) 0+0=0I think it is easy to memorize, if we remember the following rule
“all logical operation entries is similar to arithmetical entries,
but the OR operation of 1 + 1 which is equal 1 rather than 2″But we do not have to remember the rule if we just define the logical addition in term of logical multiplication and logical complementation like thisx+y == 1-(1-x)(1-y)
so all we have to remember is the first 6 entries and the definition of OR
However, it is hard to remember for a toddler who does not know arithmetic.
PEIRCEAN ARITHMETIC OF LOGIC
Now with some innovation we can reduce the 6 entries to 2 entries
if we follow a trick by Charles Sanders Peirce
the void or nothingness as the symbolic value of TRUE
the NOT(x) expression as (x)
the a AND b expression as abWith this trick we can define FALSE = NOT(TRUE) or ()
so NOT(FALSE) = TRUE can be written as (()) = .So the NoT operation table entries
(1) 1-1=0 is written as (1′) ()=()
(2) 1-0=1 is written as (2′) (())=and the AND operation table entries
(3) 1X1=1 is written as (3′) =
(4) 1X0=0 is written as (4′) ()=()
(5) 0X1=0 is written as (5′) () =()
(6) 0X0=0 is written as (6′) ()()=()See the entries 1′,3′,4’and 5′ can be forgotten because
all we have to remember is the law of identity.
Now, all we have to remember is two very simple formulas of logical arithmetic(6′) ()()=()
the NOT(x) expression as (x)
the a AND b expression as abWith this trick we can define FALSE = NOT(TRUE) or ()
so NOT(FALSE) = TRUE can be written as (()) = .So the NoT operation table entries
(1) 1-1=0 is written as (1′) ()=()
(2) 1-0=1 is written as (2′) (())=and the AND operation table entries
(3) 1X1=1 is written as (3′) =
(4) 1X0=0 is written as (4′) ()=()
(5) 0X1=0 is written as (5′) () =()
(6) 0X0=0 is written as (6′) ()()=()See the entries 1′,3′,4’and 5′ can be forgotten because
all we have to remember is the law of identity.
Now, all we have to remember is two very simple formulas of logical arithmetic(6′) ()()=()
(2′) (())=
BROWNIAN LAWS OF FORM
When George Spencer-Brown 
used it as the axioms for his primary arithmetic of the Laws of Form all he did is replacing Peircean () with his “cross”
So (6′) and (2′) can be written respectively as
which he called LAW OF CONDENSATION and LAW OF CANCELLATION
However Spencer-Brown did not plagiarize Peirce.
The primary arithmetic is the Peircean Existential Graph logic
read dually, where
is read as NOT
is read as FALSE
ab is read as a OR b
The primary arithmetic is the Peircean Existential Graph logic
read dually, where
is read as FALSE
ab is read as a OR b
He proved that all boolean tautologies can be derived from just two axioms
the Law of Contradiction
and the Law of distribution
I think this the simplest formulation of Boolean Algebra, but I am wrong.
KAUFFMANIAN BOX ALGEBRA
Replacing Brownian cross with a box notation the Spencer Brown Algebra axioms pair, as it shown by Louis Kauffman 
can be redrawn as
He also shown that both axioms can be derived from a single axiom: the Huntington axiom
+------++------+ |+-++-+||+-+ | ||x||y||||x| y | = x |+-++-+||+-+ | +------++------+
which can ultimately be simplified to its dual: Robbins axiom
In my previous blog it was shown that the Huntington axiom can be read as the ancient principle of Reductio ad Absurdum using Peircean interpretation. In fact the Robbins axiom can also be read as the same principle if we interpret it as Spencer-Brown interpreted his Laws of Form. So finally, we find the ultimate simplification of logical algebra as the most economical mathematical axiom system. That’s a wonderful discovery I got to be shared with the readers of this blog.
. Integralism 